E-courses learning and behavioral change

"Tenkende klasserom" gjør det vanskeligere for elever å lære og tenke matematisk.

Matematikksenteret, fagdidaktikere og endel kommuner har satset på metodikken "bygge tenkende klasserom" av Peter Liljedahl.

Det finnes derimot ikke en studie på læringseffekt av metoden. Det er tvert imot mange studier, som viser at denne typen metodikk gir lite læring for de aller fleste elever, og skaper større faglig ulikhet mellom elever.

"Bygge tenkende klasserom" er en ekstrem form for utforskende pedagogikk, der barna skal løse problemstillinger på vertikale tavler. Det er en blanding mellom samarbeidslæring og problembasert eller utforskende læring (lære via "rike" problemer). Ingen av disse metodene er spesielt effektive til å lære matte. Dette skal utvikle "tenkende elever" argumenteres det. Det er derimot relativt lett å måle tenkning. Det kan faktisk måles med å teste barnas evne til å løse matematiske problemer. Men, som sagt, det foreligger ikke en forskningstudie der dette er gjort. Den eneste forskningen som foreligger, er fra Peter Liljedahl selv, og måler på engasjement. Engasjement er generelt et dårlig mål på læring, og det finnes både bok-kapitler, som tar for seg "engasjement illusjonen", og eksempler fra virkeligheten, som viser at du kan ha veldig aktive og engasjerte elever, men lite læring. Man kan faktisk ikke observere læring, hvis man ikke måler på læring (tester), eller sjekker for forståelse underveis. Det er lett å bli lurt hvis man tror at elever lærer effektivt ved å være engasjerte eller aktive (motoriske). Det er mentalt engasjement, som er det fundamentale. Det elevene tenker hardt på og over, lærer de. Bygge tenkende klasserom bidrar også til det som kalles "social loafing", dvs. at enkeltelever bidrar mindre når de er i en gruppe, enn når de løser problemer på egenhånd. Delvis fordi de ikke innehar komponentene som skal til for å løse problemstillingen, for de har ikke blitt skikkelig guidet og undervist, og delvis fordi de som kan løse problemene, bidrar mest. Det er lett å observere dette fenomenet i klasserom. 
Liljedahl argumenterer altså for "tenkning" uten at det finnes tegn på at det tenkes mer ved tenkende klasserom. Det er ikke tenkning og læring vi observerer når elever løser problemstillinger på vertikale tavler. Det er aktivitet og forskjellige elevers bidrag. Det er fragmentarisk kunnskap og snakk i aksjon. Det er også stort rom for "utenomfaglig" tenkning, digresjoner og forstyrrende atferd, som tar bort fokuset fra læringsprosessen. 

"Bygge tenkende klasserom" passer med den progressive filosofien som har hegemoni innenfor utdanningssystemet, og den norske læreplanen. Det denne progressive "utforskings-leiren" derimot ikke forstår, er at vi bør tydeliggjøre innholdet elevene skal lære, for kunnskap, prosedyrer og konsepter er det vi tenker og løser problemer med. Vi bør også tydeliggjøre hvordan elevene skal organisere dette innholdet. Hvilke kunnskaper, prosedyrer og strategier kan brukes til hvilke problemtyper, og hvordan disse står i et hierarkisk forhold til hverandre, er avgjørende for hvordan du underviser. Leveringen av dette hierarkiske innholdet gjøres best ved kvalitetsundervisning, som tar hensyn til arbeidsminnets begrensninger, samt skaffoldingsteknikker, som bidrar til nok hjelp, slik at den enkelte elev kan løse matematiske problemer. Dette gjøres ikke ved "å lære via å løse problemer" underveis, lave inngangsoppgaver, der hver enkelt elev kan bidra med egne miskonsepter eller det man allerede vet (det er ikke noe læring i å bidra med det man allerede vet), eller hjernetrim oppgaver utenfor pensum på vertikale tavler. Faren for at elever utvikler miskonsepter er relativt stor med tenkende klasserom. 

Det ansvarlige alternativet til denne formen for pedagogikk er derfor:

-Eksplisitt instruksjon der konsepter og prosedyrer blir fullt ut forklart og vist. Da slipper elevene å oppfinne matte på ny, eller løse det på sin egen (ofte ineffektive) måte. Stoffet brytes ned i håndterbare enheter, og få enheter samtidig gjør at arbeidsminnet ikke overbelastes, og at det som presenteres har muligheter til å bli prosessert og faktisk lært. 

-Arbeidseksempler, som gir nok hjelp, sørger for guiding og gjør at arbeidsminnet ikke blir overbelastet i innlæringsfasen. Da slipper elevene å gjette, eller prøve og feile til riktig svar, men har en mal de kan bruke på tilsvarende problemer, som gradvis blir internalisert. 

-Etter hvert som elevene blir mer selvstendige, og de klarer å løse oppgavetypen på egenhånd, trekkes hjelpen tilbake og elevene klarer å løse tilsvarende problemer på egen hånd. 

Det finnes en fruktbar måte å tenke undervisning og metodikk på i forhold til denne  læringsprosessen. Det kalles "det instruksjonelle hierarkiet". 

La oss se "tenkende klasserom" i forhold til det instruksjonelle hierarkiet

Hvis vi legger det instruksjonelle hierarkiet, og læringshiearkiet til grunn, så går eleven først gjennom en innlæringsfase, der eleven lærer å diskriminere mellom forskjellige konsepter, kunnskaper og prosedyrer. Prosessen er langsom og famlende. Læreren bør derfor yte mye hjelp (skaffolding) og umiddelbar feedback, samt forklare og modellere i forkant. Det som dekkes er relativt snevert, og gjøres i tråd med arbeidsminneprosesser, slik at det har en sjanse til "å feste seg". Etter hvert kommer elevene over i flytfasen. Her blir kunnskapen, prosedyren og konseptet automatisert, og vi kan etter hvert se uanstrengt og kjapp og nøyaktig respondering. Dette vil mange omtale som at kunnskapen har festet seg i langtidsminnet, og dermed opptar ikke lenger noe særlig arbeidsminne, hvis det skal brukes til problemløsning. Det som dekkes er fortsatt relativt snevert, men bredere enn i innlæringsfasen. Hjelpen som ytes blir her mindre enn i innlæringsfasen, fordi eleven har oppnådd nøyaktighet. Feedbacken legges også mer etter i tid. Den er ikke like umiddelbar og direkte, som den var under innlæringsfasen. I leseopplæring kommer dette for eksempel til uttrykk ved at "flyt-trening" i form av repetert lesing er først effektivt når eleven har kanskje opp mot 97 prosent nøyaktighet, slik at det som er effektiv læringsmetodikk i flytfasen (feks repetert lesing) er ikke effektivt i innlæringsfasen, som krever en annen metodikk med fokus på fonetiske strategier, avkoding og blendingsprosedyrer med mye hjelp. Deretter kommer generaliseringsfasen, der det innlærte blir brukt med litt andre oppgaver og i litt andre settinger. Til slutt kommer anvendelsefasen, der vi kombinerer der vi har lært flytende, samt generalisert kunnskap, på mer unike måter (feks til "rike problemer" i matte). Forskjellig læringsmetodikk er effektivt til forskjellige stadier. Noe som kalles "ekspertise reverseringseffekten" er også aktuelt her, og handler om at det som er effektivt når vi skal lære noe nytt, er ineffektivt etter at vi har mestret det nye på et viss nivå. Det som er effektiv undervisningsmetodikk når vi lærer noe nytt, er altså annerledes det som er effektivt når vi kan det. 

"Tenkende klasserom" hadde hørt mest hjemme i "anvendelsesfasen", når vi kan komponentene/byggesteinene flytende og godt, hvis det var forskning som støttet det. Vi kan ikke skippe innlærings- og flytfasen og tro at vi får god problemløsning med gruppearbeid på matematiske problemstillinger gjort på vertikale tavler. Slik problemløsning krever flyt i komponent-ferdighetene. Det er flyt og generalisering, som gjør det mulig og effektivt å kombinere kunnskaper, prosedyrer og konsepter på unike måter under problemløsning i anvendelsesfasen.

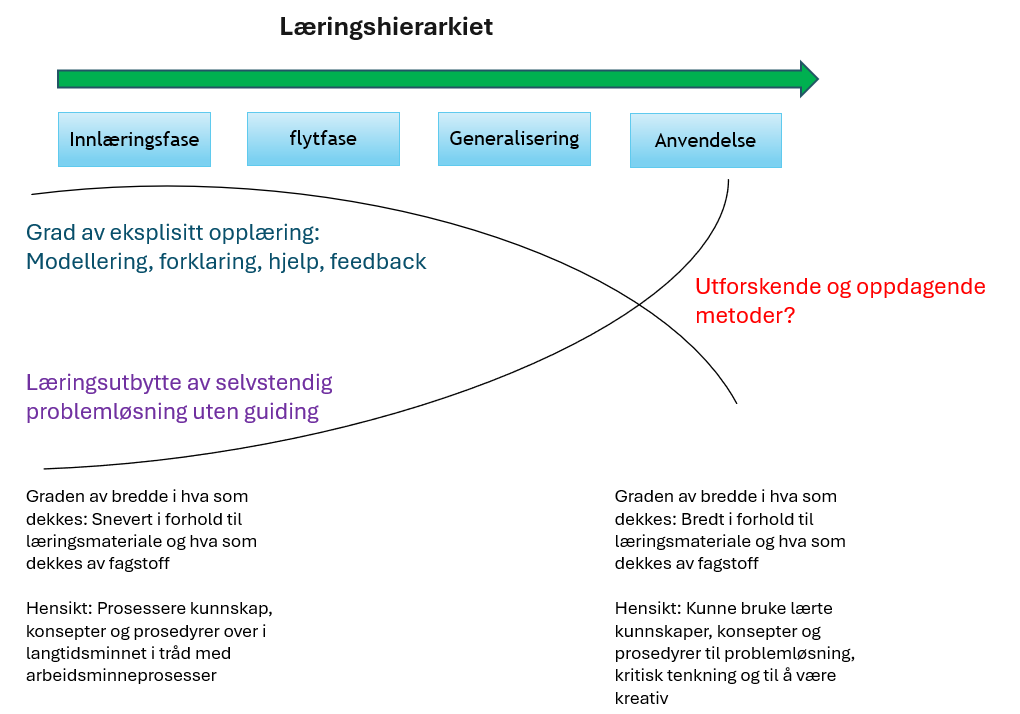
Modell av det instruksjonelle hierarkiet. Legg merke til at læringsutbytte av utforskende og oppdagende undervisningstrategier krever flyt og generalisering. En annen måte å betrakte dette på er at flyt og generalisering gjør det mulig og lettere å få til anvendelse. 

Elevene har ikke, eller får ikke, mer å tenke hardere med selv om de deles i grupper og jobber med matematiske problemstillinger.

Bruk derfor heller tiden på å levere kvalitetsundervisning av byggesteinene i problemløsning, enn rike oppgaver eller lavterskeloppgaver, som skal gjøres på vertikale tavler, der elevene underviser seg selv.

Kjerneproblemene med "tenkende klasserom" kan oppsummeres med: 
Har den enkelte elev kunnskapene som skal til for å løse problemstillingen de skal løse i felleskap sammen med andre? 
Har eleven muligheter for å skape effektive løsninger til problemstillingen på egen hånd, ut fra seg selv? 
Vil eleven ha lært noe av å ha vært bidragsyter til å løse et problem, når tilsvarende problemer dukker opp senere?

Til det førstnevnte er svaret ofte "nei". Hvis en av tre på en gruppe ikke har peiling, er det en for mye. Tiden burde heller vært brukt i felleskap til felles eksplisitt gjennomgang. 

Til nummer to er også svaret "nei". Matte er komplekst. Elever som strever, kan ikke finne på løsninger ut av ingenting, eller utvikle matte på egen hånd. Det har tatt flere tusen år og mange kloke hoder å utvikle matte.

Nummer tre vil vi ikke få greie på ved tenkende klasseroms metodikken, da det ikke foreligger forskning, og da det ikke sjekkes for den enkeltes forståelse underveis. Det finnes derimot forskning fra kognisjonsvitenskap, som viser at det er fullt mulig for enkeltelever å løse matematiske problemer, men likevel ikke lære av denne erfaringen. Grunnen er at du er så opptatt med å prøve og feile (og det opptar arbeidsminne), at du ikke legger merke til hva du gjorde for å løse problemet. Du vil kanskje heller ikke gjenkjenne den samme problemstillingen når den fremtrer igjen, og du vil derfor ikke kunne generere de samme strategier, da du ikke gjenkjenner problemtypen. Om du gjenkjenner problemtypen vil du kanskje heller ikke "huske" den løsningen du kun tidligere hadde funnet frem til ved prøving og feiling.  

Metodikken "tenkende klasserom" er ineffektiv, og sørger for få og "diffuse" repetisjoner på byggesteinene eller komponentferdighetene, som inngår i et bestemt matteproblem. 

Det er også et annet problem med "tenkende klasserom". Istedenfor at læreren "sjekker for forståelse" av hva den enkelte elev kan, eller mangler av kunnskaper for å løse en oppgave, så kan læreren umulig gjøre dette under en samarbeidsoppgave der forskjellige elever bidrar ulikt. 

At det ikke finnes kontrollert og læringsrelatert forskning på å "bygge tenkende klasserom", samtidig med at det foreligger mye godt kontrollert og læringsrelatert forskning på eksplisitte undervisningsformer, gjør det uetisk å bruke disse metodene i klasserommet. 

Derfor, bruk heller tiden som lærer på å lære eksplisitte undervisningsformer, der elevene ikke underviser seg selv. 

For mer om kritikken av tenkende klasserom: 

Podcast - chalk and talk

Norsk artikkel i bedre skole - Klara Furuberg og Jan Egil Hagen  

Artikkel Michael Pershan

Artikkel Daniel Buck

Artikkel Greg Ashman

Om det instruksjonelle hierarkiet og ressurser knyttet til dette podcast 

Hva som er problematisk med utforskende og oppdagende  undervisningsformer, som tenkende klasserom er en del av. Liljedahls tenkning representerer faktisk ikke noe historiske nytt.

Kirschner, Paul & Sweller, John & Clark, Richard. (2006). Why Minimal Guidance During Instruction Does Not Work: An Analysis of the Failure of Constructivist, Discovery, Problem-Based, Experiential, and Inquiry-Based Teaching. Educational Psychologist. 41. 10.1207/s15326985ep4102_1.